Die Mathematik der Genomevolution
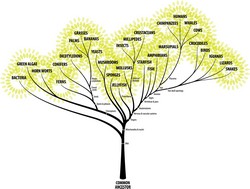
Die Vorstellung, dass alle Formen des Lebens genetisch miteinander verwandt sind, ist eine der romantischsten Vorstellungen in der Wissenschaft. Diese sogenannte Stammesgeschichte der Organismen bedeutet, dass verschiedene Arten aus früheren Formen durch Abstammung entstehen. Darüber hinaus sind alle Organismen durch eine Genpassage entlang der Zweige des Baumes des Lebens miteinander verbunden. Die Blätter dieses riesigen evolutionären Baumes entsprechen den Organismen, die heute leben. Die Wurzeln stellen die letzten gemeinsamen Vorfahren aller Arten in dem Baum dar. Forscher gehen davon aus, dass sich die genetische Information, einschließlich DNA und Proteinen, gemäß der allgemeinen Markov-Modelle von den Wurzeln aus zu den Blättern entwickelt haben. Im Rahmen des Projektes TREEMODELS (Algebraic statistics of general Markov models) untersuchten Wissenschaftler allgemeine Markov-Modelle. Diese Modellklasse enthält viele Simulationen, die in der Phylogenetik verwendet werden, um Ähnlichkeiten zwischen Pflanzen, Tieren und Mikroorganismen zu erklären. Bei diesen statistischen Modellen handelt es sich um algebraische Modelle, da sie in Bezug auf die Polynom-Beschränkungen oder Parametrisierungen definiert werden können. Die Analyse der allgemeinen Markov-Modelle basierte auf der Verwendung von algebraischer Geometrie, die es ermöglicht, Unabhängigkeiten zwischen den verschiedenen Variablen darzustellen. Algebraische Statistiken boten einen Rechenrahmen, um Probleme wie Label-Switching zu bewältigen, die die Interpretation der Ergebnisse erschweren. Das Team von TREEMODELS schlug auch alternative, einfachere statistische Modelle von Prozessen vor, die Daten aus Genomen erzeugen, und hat aus der sogenannten statistischen Inferenz Schlüsse über diese Prozesse gezogen. Genom-Sequenzen sind die Blaupause für das Leben, und doch sind ihre Funktion und Evolution weitgehend unverstanden. Diese neuen Modelle mit der Bezeichnung "Marginal Supermodels" konnten die biologische Evolution effizienter darstellen als Standard-Stammbaum-Modelle. Das Team stellte sicher, dass die Baumparameter erkennbar waren, sodass die Evolutionsgeschichte konsistent abgeleitet werden kann. Die Wissenschaftler lieferten weitere Einblicke in die Geometrie der verschiedenen Baummodelle durch die Untersuchung unterschiedlicher algebraischer Varietäten. Mithilfe von Baumkumulationen bewiesen sie, dass die sekante Varietät der Segre-Varietät torisch ist. Der Fokus lag auch auf den starken Positivitäts- und Konvexitätseigenschaften einer anderen projektiven algebraischen Varietät, bekannt als exponentielle Varietät. Algebraische Statistik ist ein neues Feld, dessen Umfang sich immer noch erweitert. Das TEEMODELS-Projekt unternahm Schritte entlang des algebraischen Statistikpfads, um Inferenztools zu entwickeln, die für biologische Sequenzanalyse notwendig sind. Mit seiner Fertigstellung soll ein wertvoller Rechenrahmen für die Organisation des biologischen Wissens entstehen.
Schlüsselbegriffe
Genom, Phylogenie, Baum des Lebens, General Markov-Modelle, TREEMODELS, algebraische Statistik
